Essere o non essere …vaccinato
Considerazioni sulla vaccinazione contro il Covid 19
Stefano Quarta
In molti avranno visto un bellissimo film del 2001, vincitore di quattro premi Oscar, con un brillante Russell Crowe nel ruolo di protagonista. Si tratta di A beautiful mind, un film sulla vita del matematico ed economista John Nash. Un uomo con aspirazioni in campo matematico ma che nel 1949, durante il dottorato, formulò la teoria che gli sarebbe valsa (45 anni più tardi) il premio Nobel per l’economia, la teoria dei giochi non cooperativi.
Questa teoria descrive bene l’egoismo intrinseco nel comportamento economico. Il fatto che individui diversi collaborino per un fine comune non è un atto di altruismo, bensì l’esatto contrario. Ognuno decide di collaborare solo per raggiungere il proprio obiettivo. Il filosofo inglese Hobbes descriveva questo comportamento con la massima latina “homo homini lupus” (uomo lupo dell’uomo), spiegando che la cooperazione sociale si basa sulla paura dell’aggressione altrui. In pratica, chiunque può uccidere qualcun altro, pertanto, un accordo che bandisca l’omicidio è vantaggioso per tutti. Ma questo accordo non si basa sull’amore per la vita altrui, bensì sul desiderio di preservare la propria vita.
Nash esamina, a mio modo di vedere, questo concetto, quantificando i risultati per i vari scenari possibili ed esponendo un metodo per trovare quello scenario che sia accettato da tutti gli attori in gioco. Questo scenario è detto equilibrio di Nash. Normalmente si utilizza l’esempio del cosiddetto dilemma del prigioniero per spiegare questa teoria. Si immagini di arrestare due sospettati di furto. I due soggetti vengono posti da subito in due stanze diverse, in modo tale che non possano accordarsi. Successivamente si procede con due interrogatori distinti, proponendo ad entrambi le seguenti pene in base alla loro collaborazione:
- Se solo uno dei due collabora, riversando la colpa sull’altro: chi ha collaborato evita la pena; chi è stato accusato viene condannato a 5 anni di carcere;
- Se i due sospettati si accusano a vicenda: vengono entrambi condannati a 3 anni.
- Se nessuno dei due collabora: entrambi vengono condannati a 2 anni di carcere per reati accessori.
Questo schema dovrebbe risultare molto familiare, perché usato molto spesso nei film polizieschi come tecnica per far parlare uno dei due sospettati. Ma vediamo come trovare l’equilibrio.
Innanzitutto, rappresentiamo con una tabella i vari scenari sopra esposti (Tabella 1).
Tabella 1 Matrice di interazione (dilemma del prigioniero).
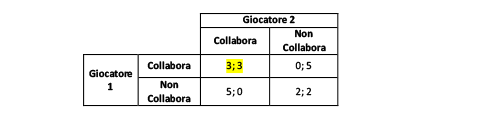
Come interpretare la tabella per trovare l’equilibrio:
- Ogni giocatore cercherà di minimizzare la propria condanna;
- Poniamo che il giocatore 1 non collabori (riga inferiore); in tal caso, il giocatore 2 otterrebbe una pena di 2 anni non collaborando e di 0 anni collaborando, quindi collaborerebbe; ma se il giocatore 2 collaborasse, al giocatore 1 converrebbe collaborare a sua volta, per prendere 3 anni anziché 5;
- Se invece entrambi collaborassero, nessuno dei due avrebbe incentivo a cambiare strategia (cioè a non collaborare), perché altrimenti avrebbero una pena di 5 anni anziché 3.
Un metodo pratico per trovare l’equilibrio è quello di confrontare, per ciascuno scenario, il primo numero in colonna e il secondo numero in riga. Se lo scenario considerato esprime i payoff migliori per entrambi i giocatori, allora è un equilibrio di Nash, cioè stabile rispetto a strategie alternative. In pratica, ogni giocatore confermerebbe la propria strategia anche dopo aver conosciuto la strategia altrui, perché la strategia alternativa sarebbe meno conveniente. Perciò, in questo caso, l’equilibrio (collabora; collabora) è l’equilibrio di Nash in quanto, per ogni giocatore, la strategia alternativa porterebbe ad una pena maggiore.
Nash ha vinto il Nobel perché questo ragionamento è applicabile e modellabile ad un’infinità di ambiti. Si immagini due imprese che debbano decidere se competere nella produzione di un nuovo prodotto. Immaginiamo che dopo attente ricerche di mercato si ottengano i seguenti payoff (i payoff sono i numeri all’interno della tabella, quindi i risultati attesi in base allo scenario):
Tabella 2 Matrice di interazione (competizione tra imprese).
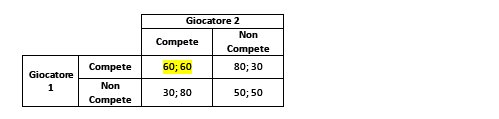
In questo caso i payoff sono i profitti attesi, quindi ogni giocatore preferirà i valori più alti. Immaginiamo che se entrambe le imprese decidessero di competere nel nuovo mercato, avrebbero dei profitti di poco superiori a quelli di partenza (situazione in cui nessuno compete nel nuovo mercato). Tuttavia, se solo una delle due imprese competesse sul nuovo prodotto, otterrebbe risultati eccezionali, mentre l’altra impresa subirebbe una forte contrazione dei profitti, dovuta a cali di popolarità o altre motivazioni. Come per il dilemma del prigioniero, anche in questo caso l’equilibrio di Nash è quello in alto a sinistra, in cui entrambi competono. Tuttavia, in questo caso l’equilibrio di Nash coincide con l’ottimo sociale, mentre nel dilemma del prigioniero no. L’ottimo sociale può essere inteso come lo scenario in cui la somma dei payoff è la più desiderabile. Sommando i payoff dei due giocatori in quest’ultimo esempio, otteniamo 120 se entrambi competono, 100 se entrambi non competono e 110 nei due scenari misti. Quindi l’equilibrio di Nash è anche quello in cui la società, che qui è composta dai soli due giocatori, ottiene il payoff massimo (o in altri termini, ottimo). Nel dilemma del prigioniero, invece, i payoff sociali sono 6 nel caso di doppia collaborazione, 4 se entrambi non collaborano e 5 negli scenari misti. Ricordando che in questo caso è preferibile un numero basso (trattandosi di una pena), si ha l’ottimo sociale nello scenario in cui entrambi non collaborano. In altri termini, ad entrambi converrebbe non collaborare ma, nonostante ciò, alla fine confessano entrambi. Per questo motivo si parla anche di paradosso del prigioniero, proprio perché i comportamenti razionali individuali contrastano con i comportamenti razionali sociali. Attenzione, i comportamenti sono in ogni caso razionali, cioè ogni individuo sceglie il meglio per sé. Cionondimeno, non ottengono il meglio per sé.
Come detto, questa teoria trova infinite applicazioni, con equilibri che possono essere di reciproca non collaborazione, oppure equilibri misti, in cui a ciascuno conviene che la propria strategia sia opposta rispetto a quella della controparte. Tutto dipende dai payoff in gioco.
In questo periodo, un’applicazione particolarmente interessante può certamente riguardare la vaccinazione contro il Covid-19 (tuttavia il ragionamento è estendibile a qualsiasi altro vaccino). I vari sondaggi mostrano come da un quarto a metà della popolazione sia tendenzialmente contrario all’idea di vaccinarsi. Ormai sono chiari a tutti gli effetti del Covid-19, sia in termini sanitari che economici. Ciononostante, una rilevante porzione di popolazione non si vaccinerebbe, preoccupata da possibili reazioni avverse. Proviamo quindi ad immaginare dei possibili payoff, in modo da costruire una matrice e vedere l’equilibrio di Nash e l’ottimo sociale. Nel fare ciò, ammettiamo l’esistenza di effetti collaterali dovuti alla vaccinazione, poiché senza questi effetti negativi sarebbe del tutto irrazionale la scelta di non vaccinarsi.
Immaginiamo che i payoff siano una sorta di punteggio di benessere che varia tra 0 e 100, preferendo quindi i valori più alti possibile. Come al solito restringiamo la popolazione a due soli individui per semplicità di trattazione e calcolo (si può comunque immaginare di essere il giocatore 1 e di avere a che fare col giocatore 2 che rappresenta il resto della popolazione). Le possibili scelte sono di vaccinarsi oppure no ma, partendo da un benessere pari a 100 in condizioni di normalità, ipotizziamo i seguenti malus:
- “-30” per gli effetti collaterali dovuti al vaccino;
- “-50” per le restrizioni che ci impone la pandemia;
- “-25” in caso di circolazione parziale del virus, con conseguenti restrizioni parziali, come risultato di una parziale vaccinazione.
Ne risulterebbe la matrice in Tabella 3.
Tabella 3 Matrice di interazione (vaccinazione pessimista).

Date queste assunzioni, entrambi i giocatori non si vaccinerebbero. Ricadremmo, quindi, nello stesso risultato ottenuto col dilemma del prigioniero. L’equilibrio stabile non è quello socialmente ottimale. In altre parole, l’egoismo di ognuno danneggia la collettività (di cui si fa parte).
Ma proviamo a ridisegnare i possibili malus, semplicemente ridimensionando il possibile danno da effetti collaterali da “-30” a “-20”. La matrice diverrebbe quella in Tabella 4.
Tabella 4 Matrice di interazione (vaccinazione ottimista).
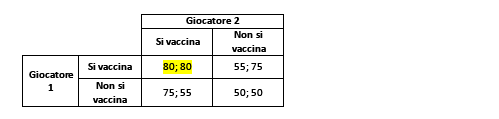
In questo caso, l’equilibrio di Nash coincide con l’ottimo sociale e prevede che entrambi i giocatori si vaccinino. Il tutto si può riassumere nella comparazione tra il danno da effetti collaterali e il danno dovuto alle restrizioni e alla malattia stessa. Siccome da un lato abbiamo a che fare con un virus che uccide, mentre dall’altro vi sono dei vaccini che dovrebbero avere i soliti effetti collaterali che si limitano a pochi giorni di malessere, non vedo come si possa considerare valida l’ipotesi in Tabella 3.
Per far si che alla fine i vaccini risolvano questa crisi pandemica, occorre che una percentuale rilevante si vaccini. Per diverse malattie si fissa al 95% la quota di sicurezza per raggiungere la cosiddetta immunità di gregge. Tuttavia, per il Covid-19 ancora non si conosce quale possa essere il livello minimo da raggiungere. Al momento non si rende necessario l’obbligo di vaccinarsi perché le dosi disponibili sono molto poche ma in estate, al raggiungimento di una disponibilità di dosi rilevante, sarà certamente opportuno valutare delle misure che, anche obtorto collo, permettano di raggiungere questo livello minimo necessario. Per il momento, resta solo da sperare in una corretta valutazione dei vari “effetti collaterali” da parte della popolazione ricordando che, un po’ come per l’astensionismo dal voto, chi elude i doveri, rinuncia ai diritti.



